攻防世界 —— Crypto（进阶区1）

0x00 前言

更新完Crypto新手区的题目之后，接下来开始练习进阶区的题目。本系列文章持续更新中~

0x01 告诉你个秘密

解题思路

打开附件发现为两行十六进制数据，一开始考虑将其转换成十进制，后来发现转完之后不易和字符串建立联系，遂考虑直接将其转换为字符串。

这里使用python的binascii库中的binascii.a2b_hex(hex)实现将十六进制字符串转换成ASCII字符串并输出。输出结果显然为Base64加密，直接解密得到如下结果：

乍看是一堆无意义的字符串，但注意其使用空格作为分隔符分开，考虑到键盘密码，与键盘上的字母对应得到最后的flag。注意本题flag的格式直接为最后得到的字符串，没有任何前缀。

解题脚本

import base64
import binascii
cipher1 = '636A56355279427363446C4A49454A7154534230526D6843'
cipher2 = '56445A31614342354E326C4B4946467A5769426961453067'
final_plain = binascii.a2b_hex(cipher1) + binascii.a2b_hex(cipher2)
final_plain2 = base64.b64decode(final_plain).decode()
print(final_plain2)

一些经验

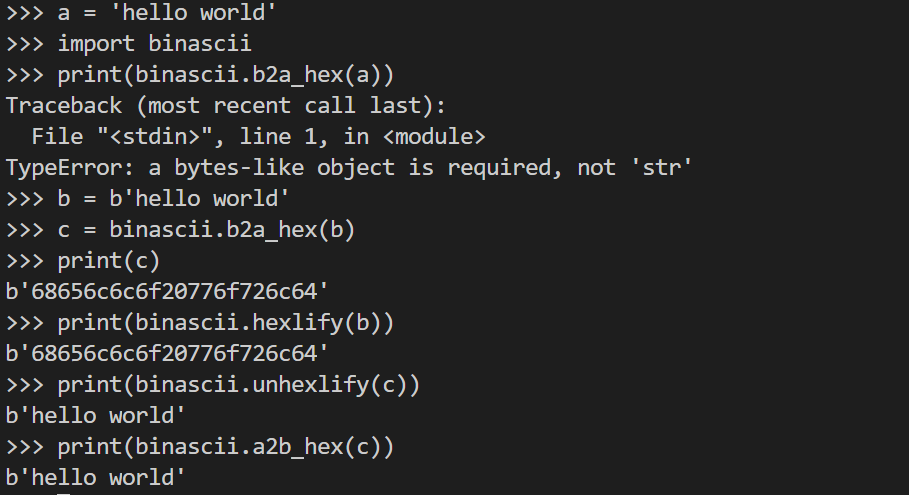
下面来讨论一下使用binascii库进行ASCII字符串与十六进制字符串转换的细节。

由上图可知，在ASCII字符串与十六进制字符串转换过程中，binascii库提供了四个函数。

我们可以使用binascii.a2b_hex(hex_string)和binascii.unhexlify(hex_string)这两个函数实现从十六进制字符串到ASCII字符串的转换过程。可以使用binascii.b2a_hex(ASCII_string)和binascii.hexlify(ASCII_string)这两个函数实现从ASCII字符串到十六进制字符串的转换过程。值得注意的是，在python3中，互相转换的数据类型为byte型而非string型，否则就会出现TypeError报错。

0x02 Broadcast

解题思路

本题目提供了加密脚本task.py，Bob、Dan、Carol和Erin的pem与enc文件。单独看这道题目确实很简单，因为flag直接包含在题目给出的脚本中。但是如果对题目提供的加密方式进行挖掘，可以得到许多有趣的信息。

题目名字为Broadcast，实际上并不是简单的广播攻击。对于RSA的简单广播攻击，其前提是对同一个m加密，攻击细节如下图：

分析加密脚本中对待加密信息的处理过程：

data = {'from': sha256( b'Alice' ).hexdigest(),
        'to'  : sha256( name.encode() ).hexdigest(),
        'msg' : msg
       }
data = json.dumps(data, sort_keys=True)
m = number.bytes_to_long( data.encode() )

显然每一次的m不同，并且取e=3和e=5时分别只有两个其他明密文对，无法使用应对传统广播攻击的方法进行处理。

观察可知，每次m都由以下内容构成：

• from Alice（每次相同）
• to name（每次不同）
• msg（每次相同）

其中只有to: name每次变化，而另外两个参数保持不变。由于引入语句data = json.dumps(data, sort_keys=True)，在加密之前会根据data字典的key进行排序，由于三个键的首字母排序为from-msg-to，可以发现msg被放到中间位置。即m = high + mid + low。

对于每次构造的信息m，其高、中位('from':Alice，'msg': msg)都是不变的，只是低位由于每次接收方不同有所不同。由于high和low已知的（可以通过构造过程中提供的方法进行计算），我们只需要求出mid部分即可。

由于low部分包含64位的sha256摘要信息以及12位其他符号，故构造m如下：

$$m_{i} = (high << 1368) + (x << 608) + low_{i}$$ $$m_{i} = a*x*2^{608} + b_{i}$$

其中a = 1, $b{i} = high*2^{1368} + low{i}$

且x仅为95*8=760位

此时可以利用Broad Attack with Linear Padding结合Copper Smith Attack进行求解。

构造多项式$f(x) = (x*2^{608} + b) ^{3} - c (mod n{1}n{2})$的small root。

需要注意的是，small root要求小于模数n的1/e次方，而x为760位，7603 = 2280 > 2048 = 10242，所以需要使用两组加密信息使得模数的位数增大为4096位，从而760位的x满足small root的条件。

解题代码

根据以上分析，根据给出的pem和enc文件提取两对使用3作为加密指数的(n, c)对，编写sage脚本解密如下：

from functools import reduce

n = [11743537468135317101480488020144809201914936988461977176868954193874417724397531738707729413940060004291802011501577549223271797288223565654061393379024948557114873802484065401046235691942131446370168987779343797500311519782297945918303703564655987952282482715476136773764831205732478344688915636069116516770855051840466960976764092858799500910720099908106249684080240663853178927556249049193503151085654884527269002477666950572742679984293662085069728877459286849951188181117702216469759179036558783079196215512501682142798495265635852347494193629555160491782509569392767123686061925883459482937083314597325931324903,
    14457209969884668177708697333084651442256193118762305783886170334587420837310297145702128170106972242068185696834421424217621080232658721763477597612126355466640947700608787202555955170003838596141926637700553638034795412618607691704863949191711837596504911369550275265047485577345602266210861036695691235637536527380239331718278464709412846966181787795995822367966392084870050879397930114908541580226650851547317522603090899886280170245299959983054236157294287800393659291904879499563552223080590816177114742527572796924746954499447982388532224932540152177949556088321209870823140903366811600475984145194404542130227]
c = [8190049298225986645065639656298172597926128706450768371303258134744480067344252838541490888036183464705944304534788993901104793815361341756431217860700928158019252752618919437673052832128577726977953950790902559970309709239504865249701468783648614158118356226876181834829777260079340923537145106302704145961190836661375363413110097880213997662546161624163926197325967768410253429584704238310212909716376684130921549808859640649278922277248496022978656354003386568276074858346316327173050731369576404526308212891898482132494538059251451015302281630189059974681450654073047538089109981563439870031087270051532901896822,
    12118101166054737713386215385862569765107262982956699621223784645643668203345111850159614142861485707244381466506582226100758646240135249724760825645393433062905277245716757630096083674730526877271237776864887538290354358982569685278734177038607779153674199245850037034568957234569159850767151815484600506473286544739506911281943726669304436835800686344966600632518764992677531015390701093253398220813342080495059893716294823513371481710159387645437923515728187314225175839309059255201792376404426500260584133880852811820804606509557432184294402579927159295465411669899092463872169344366863225658285149101653314280770]
a = [1, 1]
# b_i = high + low_i
b=[15544274873612998989866379328566946388285248570806564503108352867340017880252665817613208325183832507901409765669821491355202065667225050801744228447515864518584620720787409961012061302114074543857882368586098987225919736280924738224995075370843988377198544539266275729089636607095220506662375139381261384398438998662059177913249680151096549632879238896603189241688956490787338355571799212913598318011639865738648621731434747681682396930715043552472778331701738091587062917693835229391950847730617837543337471998802061973389340720433170042633451884844390746043635079083497185464124715717119052915013438803576714502781,
   15544274873612998989866379328566946388285248570806564503108352867340017880252665817613208325183832507901409765669821491355202065667225050801744228447515864518584620720787409961012061302114074543857882368586098987225919736280924738224995075370843988377198544539266275729089636607095220506662375139381261384398438998662059177913249680151096549632879238896603189241688956490787338355571799212913598318011639865738648621731434747681682396930715043552472778331701733991049485714120357663081338580983163588987883815040112341393183479429685436337175694444720513269496978577270272192766705854550355666404326847416678342795901]

def chinese_remainder(n, a):
    sum = 0
    prod = reduce(lambda a, b: a * b, n)
    for n_i, a_i in zip(n, a):
        p = prod // n_i
        sum += a_i * inverse_mod(p, n_i) * p
    return int(sum % prod)

T = []
T.append(chinese_remainder([n[0],n[1]],[1,0]))
T.append(chinese_remainder([n[1],n[0]],[1,0]))


N = n[0]*n[1]
P.<x> = PolynomialRing(Zmod(N))

g=0
for i in range(2):
    g += ((a[i]*x *2^608 + b[i])^3 - c[i])*T[i]
g = g.monic()
x = g.small_roots()[0]
print x
print hex(long(x))[2:].strip('L').decode('hex')
# 1714661166087377473014475529806516832214035482305327415277479703776481564871479523924321275498885242003713793314464965569235093750357822116766965311615937698169583931123673327349849371866141948995747458407120138743748898874096942
# Hahaha, Hastad's method don't work on this. Flag is flag{6b6c9731-5189-4937-9ead-310494b8f05b}.

0x03 cr3-what-is-this-encryption

解题思路

该题以十六进制明文的方式给出了p, q, e这三个RSA解密需要的参数以及密文c，直接编写脚本解密即可。需要用到gmpy2和binascii这两个库。

解题脚本

import gmpy2
import binascii
p='0xa6055ec186de51800ddd6fcbf0192384ff42d707a55f57af4fcfb0d1dc7bd97055e8275cd4b78ec63c5d592f567c66393a061324aa2e6a8d8fc2a910cbee1ed9' 
q='0xfa0f9463ea0a93b929c099320d31c277e0b0dbc65b189ed76124f5a1218f5d91fd0102a4c8de11f28be5e4d0ae91ab319f4537e97ed74bc663e972a4a9119307' 
e='0x6d1fdab4ce3217b3fc32c9ed480a31d067fd57d93a9ab52b472dc393ab7852fbcb11abbebfd6aaae8032db1316dc22d3f7c3d631e24df13ef23d3b381a1c3e04abcc745d402ee3a031ac2718fae63b240837b4f657f29ca4702da9af22a3a019d68904a969ddb01bcf941df70af042f4fae5cbeb9c2151b324f387e525094c41'
c='0x7fe1a4f743675d1987d25d38111fae0f78bbea6852cba5beda47db76d119a3efe24cb04b9449f53becd43b0b46e269826a983f832abb53b7a7e24a43ad15378344ed5c20f51e268186d24c76050c1e73647523bd5f91d9b6ad3e86bbf9126588b1dee21e6997372e36c3e74284734748891829665086e0dc523ed23c386bb520'

p_decimal = int(p, 16)
q_decimal = int(q, 16)
e_decimal = int(e, 16)
c_decimal = int(c, 16)
phi_n = (p_decimal-1) * (q_decimal-1)
d = gmpy2.invert(e_decimal, phi_n)
m_decimal = pow(c_decimal, d, (p_decimal)*(q_decimal))
final_message = binascii.a2b_hex(hex(m_decimal)[2:])
print(final_message.decode())

0x04 flag_in_your_hand1 & flag_in_your_hand

解题思路

这两个题的思路和flag都是一样的（小声逼逼

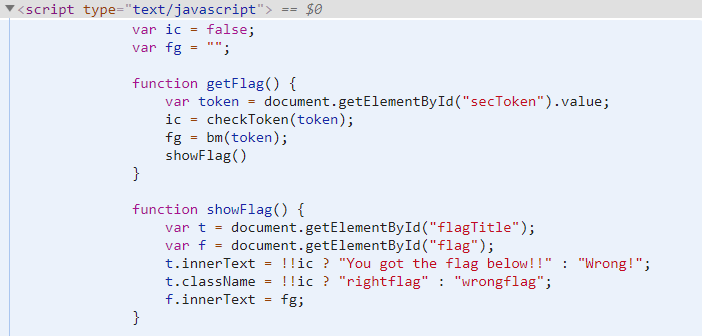
下载附件并解压，文件夹中有一个html页面和一个js脚本。首先进入页面，容易得到flag的获取流程为：手动输入Token，并运行getFlag()函数，步进查看该函数细节。

可以很清楚地看到，该函数首先获取输入框中的Token值，并将其传入checkToken()函数，返回结果为ic，然后将其传入bm()函数，该函数返回结果为fg。进入提供的js脚本中查看这两个函数，可以发现bm()函数与flag的生成过程有关，分析可以得到其运用单表替换的编码方式。单独查看checkToken()函数可以发现其返回结果为false。但结合bm()函数的运行流程可以发现，ic的值会通过ck()函数覆盖。

观察ck()函数内部可知，其检验过程要求输入Token中每个字母的ASCII值与数组a中的对应位置ASCII值相差3，于是可以编写脚本得到验证正确的Token，输入以获得flag。

解题脚本

password = ''
a = [118, 104, 102, 120, 117, 108, 119, 124, 48,123,101,120]
for item in a:
    password += chr(item - 3)
print(password)

0x05 工业协议分析1

解题思路

下载附件后发现其为pacap文件，记录网络流量。使用wireshark打开后，追踪TCP流，在结果中搜索flag字符串，发现flag.txt字样，考虑网络流量中包含与flag相关的txt文件。

在命令行中搜索发现flag.txt结果不存在有意义的明文，遂搜索其他可能发送的文件类型：

grep ".txt" -a sample.pcap
grep ".rar" -a sample.pcap
grep ".zip" -a sample.pcap
grep ".png" -a sample.pcap

当搜索png图片相关时，发现网络环境中传送了base64加密的图片。

编写脚本解密即可得到flag。

解题脚本

import base64
# 将上图中的base64加密结果存入./final_result.txt文件中
base_result = open('./final_result.txt', 'r')
png_result = base_result.read()
png_after_decode = base64.b64decode(png_result)
result = open('./result.png', 'wb')
result.write(png_after_decode)

0x06 你猜猜

解题思路

下载并打开题目给出的附件，发现其开头为50 4B 03 04显然是zip格式压缩包的开头，我们将其复制粘贴到Winhex中，注意保存的时候选择ASCII Hex选项，可以看到其ASCII字符以PK开头并且内部包含flag.txt。

将该压缩包解压发现需要密码，首先考虑zip伪加密发现不符合要求，于是使用密钥爆破软件进行爆破，得到最终密码为123456，解压得flag。

一些经验

先知社区有一篇非常详细的手撕压缩包过程，对压缩包结构的理解有一些帮助：从做CTF题到手撕ZIP。

0x07 fanfie

解题思路

攻防世界上的题目既没有提示也没有flag格式，直接给了一堆看上去像base32编码的字符串，完全没有思路。于是找到原题得到两个重要提示。这样我们有如下题目条件：

1.flag的格式为:BITSCTF{}
2.Brute and get the base 32 format of flag
3.encrypted.txt : MZYVMIWLGBL7CIJOGJQVOA3IN5BLYC3NHI

可以看到题目提供的密文是对base32加密结果进行未知方式加密的结果。所以我们需要将提供的密文先还原成base32加密的结果，再进行base32解密得到最终flag。

base32转换过程中将明文按照每五个字符为一组进行分组，将结果进行base32加密后长度填充为8的倍数。由于已知flag以BITSCTF开头，我们取前五个字符进行base32加密，得到结果为MZYVMIWL，看起来该未知加密方式为单表替代加密。构建字母表并寻找对应关系如下：

整理得到如下关系式：

3->11
4->24
8->12
9->25
20->8
21->21
26->22

假设为仿射密码，可以解出a = 13, b = 4, modulus = 27，编写脚本解密后将结果进行长度填充至8的倍数，再进行一次base32解密即可。原来这个题目的名字进行移位之后会变成affine啊（小声逼逼

解题脚本

import base64
import gmpy2
str = 'BITSC'
print(base64.b32encode(str.encode()))
a = 13
b = 4
mod = 32
a_modinv = gmpy2.invert(a, mod)
print(type(a_modinv))
base32_result_after_encode = 'MZYVMIWLGBL7CIJOGJQVOA3IN5BLYC3NHI'
alphabet = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ234567'
base32_result_after_decode = ''
for item in base32_result_after_encode:
    index = alphabet.find(item)
    base32_result_after_decode += alphabet[a_modinv*(index - b) % mod]
print(base32_result_after_decode)
flag = base64.b32decode(base32_result_after_decode+"="*6)
print(flag)

0x08 wtc rsa bbq

解题思路

拿到该题目的附件并解压，发现其包括key.pem和cipher.bin，说明密钥以证书的形式存在，而加密结果以二进制文件的形式存在。

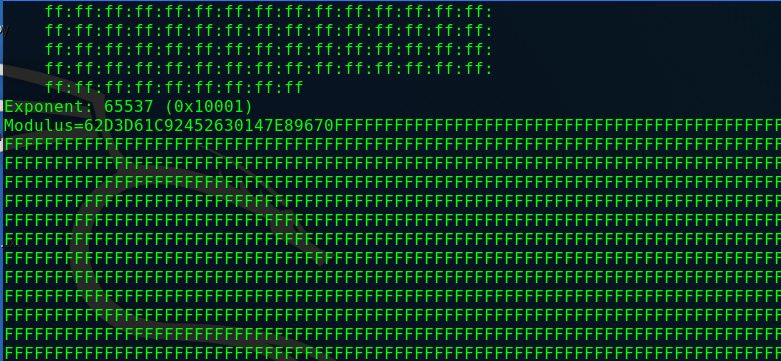
进入到Kali中使用系统自带OpenSSL的命令：rsa -pubin -text -modulus -in warmup -in key.pem，获取公钥对如下：

可以发现其模数N非常大，e为标准加密指数。编写脚本将密文以十六进制的形式从cipher.bin中读出。

ciphertext = open('./cipher.bin', 'rb').read().encode('hex')

至此，解密数据的提取过程完成。

整道题目没有其他可以操作的参数，我们只能分解模数。观察模数N，发现其位数较多，显然直接分解这条路行不通（指factordb，这里使用yafu的话理论上是可以跑出来的，我们考虑费马分解法。

费马分解法适用于RSA加密过程中选取的大素数p,q较为相近的情况，运用到了|p-q|这一参数较小的原理进行爆破，从而实现分解模数N的功能。编写费马分解函数将N分解之后即可正常解密得flag。

解题脚本

import math
import gmpy2
import binascii
def fermat_resolve(N):
    B = math.factorial(2**14)
    u = 0;v = 0; i = 0
    u0 = gmpy2.iroot(N, 2)[0] + 1
    while(i<=(B-1)):
        u = (u0+i)*(u0+i)-N
        if gmpy2.is_square(u):
            v = gmpy2.isqrt(u)
            break
        i = i + 1
    p = u0+i+v
    return p
def decode():
    decimal_e = 65537
    n = '62D3D61C92452630147E89670FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF'
    decimal_n = int(n, 16)
    p = fermat_resolve(decimal_n)
    q = decimal_n // p
    print('p = ' + str(p))
    print('q = ' + str(q))
    phi_n = (p-1) * (q-1)
    d = gmpy2.invert(decimal_e, phi_n)
    ciphertext = '04940e995809b8346a7225a4ef8f175ef3031d33f975b5398cae11e0accb9195c4e351274bb9dbac1d1b9819ae679e8d300457f3e5f8f31150648f8393cbf503e40b11140b8a8a51d22bc5bc74fdbfda0e8dabcc6704d128aa29fe480538801bd4de422e6f1a221e471f75d855a49033289e1f58e0db5e8d2a2dab473912b1b35ed0552890c8b73246266c27edb90b1509a2d5d209236e23050c45acf812df98b1be3a8bcdff9891c773daa17b72db3fd59cd2b65ee103ec7b24e1358ebe14ccb86831a617df10674dd842939ddd455e741d4fc8f1421917b782d1660651a5396928a94661bcdf9f0d2f956fc6ca238478ef44701eefb3b0e5610dd5562fce66be11b1b5d9ffca636a52037d7ce6cd44ea810ba84c49c02ae29bd2de3ffa03ae8f05b3e633f0f11c513528f1404c66217b9d5605e6f0869c25bf024b93ce35aef2ab16d0f14f34c850ec1d13c73e46bd58686903bf63740142579095d7d293f8bd35abf653729ecd0e84954a73a07d8504ca03d3aa44a6b08d776ecf8949c5b71d52e2000ebd6610a3e18f7f739e4958e070ec9b9c9493c990d637850d2aad752fb60859f676a76fc1f3e2956abedd2bdb8eb49f88ac0b9ae01d3c848187536803c7a99e61e9e4d9e10ad60952e9387b4242c24d06f3fdb247f4c8b85425b49a8db6a716144a0e62273cb722709f96f9c254eae9d5fc9b1a0abae30af9da49af765572908251e99beaf1605a40043b7ce8cfbdd49cdbc33c0216d966165a5f04599db3dcc2404139249be6cae78b5794293451a6902c18b7719759475b31b976e40c8d579f84202808836f5ddf04d4a1edf22555c7612df1973e45b343045d02b5a90a760cebb69ef862ffe2c023ee3ee5f3968c07120e9b8d036fdeccaed9f1b7ce678f44c3e507bf5015751078f990efe248fef787f34570134679207d599cab2d58524265167d3af2208325a671f9a0ced94b902121eaa6ee982d4c23b543f863580291aab134fea82c9a711d12d2bc19efa168c05be070258442c46da95ab6f1dbf5bef845fa48524ebcda31d5e19ccb69835bd50812ef0117ff33f4319072f94359cb69eb951133afb2d72e2773a5480d04969389153d831be6007915c571f8817d6d56ed6ed5dfda5d855e4ddab32ecfdabc2b5d2235712d13226093bdac6c7c283415cdde559b638d42a19ca97a842c01bf88bdc3ec55f71dcce5b0dad2527004601ae2b49c5c1a13ecfb7e7170938382b77724c208aed8d7cb1fb23a28596c1e43b64d46336c10dae18146faf4d5eb8c42c167410903d76f80fdde479beffb56a07bb9cef7a559579b637d625b783e74c495c495b162a98340c11ccdc3fd6a127f163757f94cbffc4542b913e993258ffdf85f7b04be637126dc195a7a6910d942cc870214a198a5e984a44a92c0827786515280bf7379bebdefe579c7e5a9a69116f603911d01010d1ca93882c8fe4791bf580a60731444eb09f1f50fca0ddfb9d99310a9ed699551eb17c16433'
    c = int(ciphertext, 16)
    plaintext = int(pow(c, d, p*q))
    message = binascii.a2b_hex(hex(plaintext)[2:])
    print(message)

if __name__ == "__main__":
    decode()

一些经验

当题目只给出一个加密过程（广播攻击不适用）且其他参数没有明显可以攻击的特征时，我们只能考虑直接分解模数N。对于模数N的分解，我们常使用两种方法：借助大整数分解网站和使用Windows自带的工具yafu。前者只适合分解一些初级题目中位数较小的模数，后者包含多种模数分解方法，但效率较低。除此之外我们可以参考GitHub上的CtfRSATools这一项目，其中模数分解环节提供了许多常见的分解算法。

所有分解算法中，费马分解法和Pollard p-1分解法。下面简要介绍这两种分解方法并给出分解脚本。

费马分解法

该方法适用于构成模数N的两个大素数p,q相近即|p-q|较小的情况。过程如下：

任何一个正整数n都能拆成$n = 2^{k} a$的形式，其中a为一个奇数。若$a = cd$，则令$x = (c+d)/2$，$y = (c-d)/2$，则$x^{2} - y^{2} = a$，枚举$x^{2}$观察$x^{2}-a$是否为完全平方数，如果是，则$c = x+(x^{2}-a)^{(1/2)}$和$d = x-(x^{2}-a)^{(1/2)}$就是a的因子。我们通过枚举$x^{2}$可以找到a的所有因子。

代码如下：

import gmpy2
def fermat_resolve(N):
    B = math.factorial(2**14)
    u = 0;v = 0; i = 0
    u0 = gmpy2.iroot(N, 2)[0] + 1
    while(i<=(B-1)):
        u = (u0+i)*(u0+i)-N
        if gmpy2.is_square(u):
            v = gmpy2.isqrt(u)
            break
        i = i + 1
    p = u0+i+v
    return p

Pollard p-1分解法

Pollard p-1方法由Pollard提出，适用于p-1或q-1能够被小素数整除的情况。具体流程如下：

代码如下：

import gmpy2
def pollard_p(N):
    B = 2**20
    a = 2
    for i in range(2,B+1):
        a = pow(a, i, N)
        d = gmpy2.gcd(a-1, n)
        if d>=2 and d<=(n-1):
            q = n // d
            n = q*d
    return d

0x09 工业协议分析2

解题思路

该题目给出pcap附件，可以想到为流量分析，使用wireshark打开，发现存在关于ARP、UDP、SNA协议的流量包以及大量的UDP流量包。

观察UDP流量包的长度，可以看到有些长度仅出现一次，其余长度多次出现。于是猜测这些流量包存在异常。分别分析这些流量包，发现长度为147和179的流量包出现异常字符串：

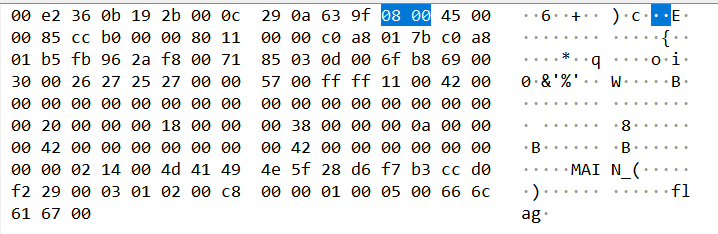
长度为147的流量包传输的数据以flag结尾。故推测下一个从192.168.1.123向192.168.1.181发送的流量包可能包含flag信息。果然从长度为179的数据包中发现可疑数据：

将末尾的十六进制字符串转换为ASCII字符串可得flag。

0x0A 工控安全取证

解题思路

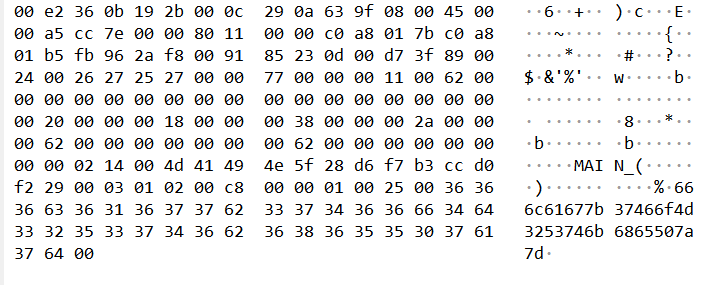
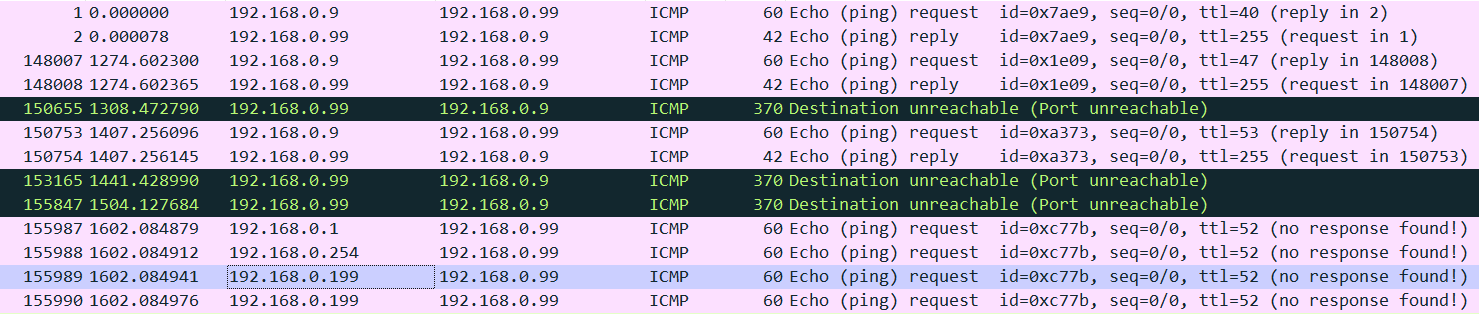
题目给出.log文件并要求查找发起第四次扫描时的数据包编号。使用wireshark打开，发现有UDP，ICMP和TCP三种类型的数据包，并存在大量的TCP流量。

观察发现，UDP流量只有三条记录，TCP流量记录过多，显然第四次扫描时的数据包不在这两类流量中。接着分析剩下的ICMP数据包，可以看到每次发送大量TCP数据包之前，先发送ICMP数据包。找到第四次建立连接发送的ICMP数据包，其编号为flag。

0x0B 小结

这十道题目里面需要特别注意的是第二题Broadcast和第八题wtc rsa bbq。前者提供了一种与普通RSA广播攻击不同的情形，引入了Hastad Attack以及Broadcast Attack with Linear Padding，并且其结合sagemath编写的解题模板值得借鉴。后者考察了只提供一对(c, n, e)情况下对参数n的处理，除在线网站及yafu分解外，还可以考虑Fermat Resolve和Pollard p-1 Resolve，注意二者适用的p,q对应情况。

以及，高校战疫的Crypto题目真的好少。pwntools杀我，这辈子都不想再看到EOFError了！